Speeding up Simhash by 10x using a bit hack
The SimHash algorithm, introduced in 2002 by Moses Charikar, can compute fingerprints of sets with the property that similar sets lead to similar fingerprints. By considering only the precalculated fingerprints, the cosine similarity between corresponding sets can be quickly estimated from the fraction of equal bits which allows accelerating tasks such as searching or grouping similar sets.

The algorithm can be applied whenever objects can be represented as sets and the corresponding cosine similarity metric is appropriate to measure the similarity of the original objects. Even if objects do not have a natural set representation, they can often be mapped to a set. For example, text or binary documents can be viewed as a set of tokens, graphs as a set of edges, or GPS routes as a set of crossed cells in a rasterized map. Examples of real-world applications include website deduplication or web tracking.
How does it work?
SimHash is actually quite a simple algorithm. To calculate the fingerprint of a given set, the hash values of its elements are combined in a special way. A 1-bit in the fingerprint indicates that the bit is set at the same position in the majority of element hash values. Otherwise, if the majority of bits at a certain position are unset, the corresponding bit in the fingerprint is 0. The figure below demonstrates the computation of the fingerprint for a quote by Steve Jobs represented as set of words {“creativity”, “is”, “ just”, “ connecting”, “things”}.

If the number of elements in the set is even, it is possible that there are as many zeros as ones. To resolve ties and prevent a bias, one can, for example, set the bit to 0 or 1 depending on whether the bit position is even or odd.
It is easy to understand why SimHash provides similar fingerprints for similar sets. For large sets, adding or removing a few elements hardly changes the majority ratios, and most bits remain the same. Identical sets obviously lead to identical fingerprints corresponding to 100% coinciding bits. In contrast, for disjoint sets that have no common elements, the bits of both fingerprints are completely independent. However, 50% of all bits can be expected to coincide by chance. The collision probability for a single bit is roughly a function of the cosine similarity with a value range between 50% and 100%. This in turn allows estimating the similarity based on the fraction of identical bits, with the estimation error scaling inversely with the square root of the fingerprint length.
More accurate similarity estimates or indexing techniques like locality-sensitive hashing require fingerprint lengths that exceed the typical element hash length of 64 bits. Concatenating the output of multiple independent hash functions would be one way to obtain longer element hashes and thus longer fingerprints. However, a more convenient approach is to compute only a single hash value per element used to seed a pseudorandom number generator. Then a random bit sequence of arbitrary length can be generated and used as the element hash for the SimHash calculation.
To determine the bitwise majorities, a count array is usually used, with a size equal to the number of bits in the fingerprint to be calculated. For each bit position the number of set bits is counted. After processing all elements, the corresponding bit in the fingerprint is set (unset) if the corresponding count is greater (less) than half the number of elements in the set. Processing a single element means iterating over the bits of its hash value and incrementing the corresponding counter if a bit is set. The following figure shows the processing steps for a single element when counting the number of set bits.
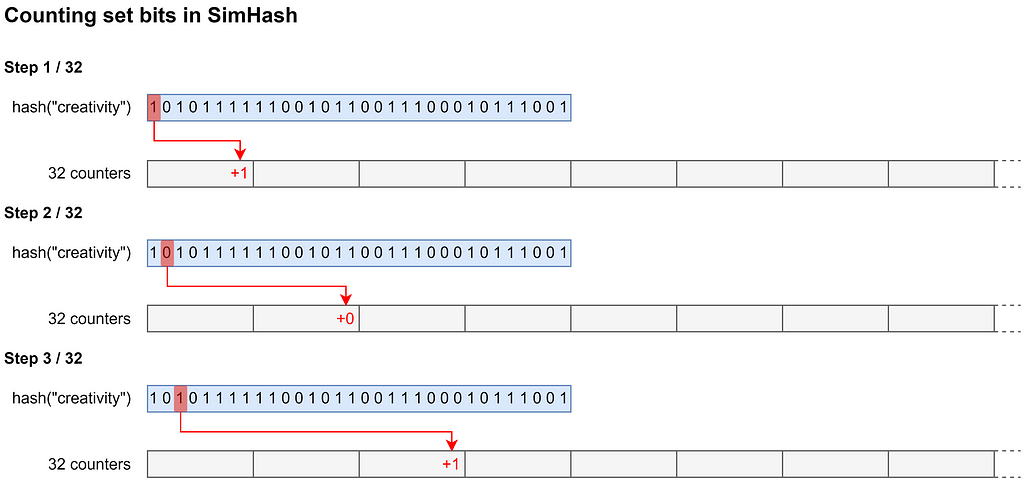
The bit hack
Especially for larger fingerprints, the individual processing of hundreds or even thousands of bits becomes very slow. Our idea is therefore to process multiple bits simultaneously in a single processing step. For this purpose we use each byte of a word as an individual counter. So a single 64-bit word can be used for counting the number of 1-bits at 8 different bit positions. Obviously, the range of those counters is limited to [0, 255]. To prevent overflows, the 8-bit counters are transferred and added to another larger counter array after every 255th processed element. Then, after the 8-bit counters have been reset by simply setting the entire word to 0, counting can be continued.
This new way of counting allows updating the counts for multiple bit positions at once by masking every 8th hash bit of a word and simply adding the result to the word containing the corresponding 8-bit counters. We repeat this for every 8th bit with other offsets, first shifting the hash bits to the right accordingly. After all 8 possible offsets have been processed, all set bits of the first word of the element hash are counted and we can proceed to the next word of the element hash. The procedure for counting the set bits of a single element is illustrated in the figure below for an assumed word size of 32 bits.
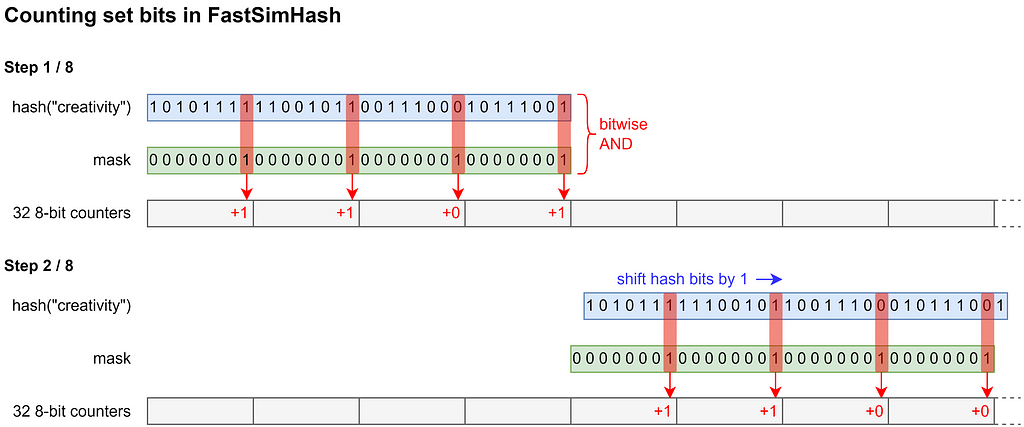
The resulting algorithm, which we named FastSimHash, uses a different association of bit positions to counters leading to a different fingerprint than SimHash. However, as the same permutation is applied to all computed fingerprints, their relative statistical properties remain the same, and they can be used in the same way. FastSimHash requires less steps to process a single element. For 32-bit words, the number of processing steps is reduced by roughly a factor of 4, and for 64-bit words even by a factor of 8, which should lead to a significant performance gain.
Benchmark results
We ran some benchmarks, where we measured the computation time for different fingerprint and set sizes. The measured times also includes the generation of a list of 64-bit random values which were used as input instead of the list of element hash values. The figure below shows the JMH benchmark results obtained on an AWS c5.metal instance with disabled Turbo Boost (P-state set to 1).
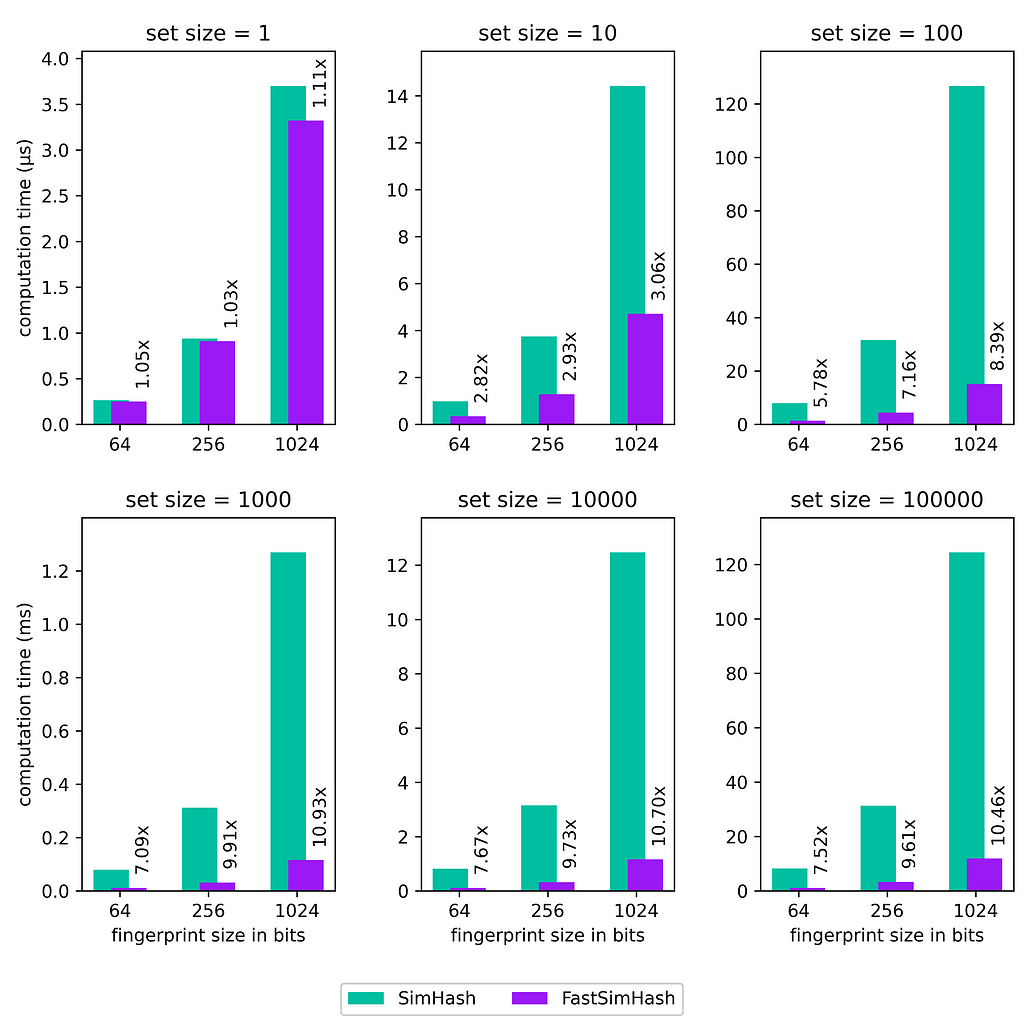
Although we need to copy the counts after every 255th element, the performance gain is huge and is roughly an order of magnitude for larger set and fingerprint sizes. While a factor of up to 8 was somehow expected for a word size of 64, FastSimHash is sometimes even faster reaching speedup factors of 10x. The 8-bit count array provides an additional performance boost as its smaller size improves data locality compared to the 32-bit count array commonly used in SimHash implementations.
Curious now?
If you want to try FastSimHash yourself, have a look at our open source Java library Hash4j. It contains an easy-to-use implementation of FastSimHash and also SimHash for comparison. The code snippet below demonstrates the computation of fingerprints for 3 different sets, followed by pairwise comparisons. While the percentage of identical bits is close to 0.83 for the very similar sets A and B, this number is close to 0.5 for the disjoint sets A and C and B and C, as expected.
// define sets
Set<String> setA = Set.of("small", "set", "of", "some", "words");
Set<String> setB = Set.of("similar", "set", "of", "some", "words");
Set<String> setC = Set.of("disjoint", "collection", "containing", "a",
"few", "strings");
// configure similarity hash algorithm
SimilarityHashPolicy policy =
SimilarityHashing.fastSimHash(1024); // fingerprint takes 1024 bits
SimilarityHasher simHasher = policy.createHasher();
ToLongFunction<String> stringHashFunc = // define hashing of set elements
s -> Hashing.komihash5_0().hashCharsToLong(s);
// calculate fingerprints
byte[] fingerprintA = simHasher.compute(
ElementHashProvider.ofCollection(setA, stringHashFunc));
byte[] fingerprintB = simHasher.compute(
ElementHashProvider.ofCollection(setB, stringHashFunc));
byte[] fingerprintC = simHasher.compute(
ElementHashProvider.ofCollection(setC, stringHashFunc));
// compare fingerprints
double fractionEqualBitsAB = // 0.830078125
policy.getFractionOfEqualComponents(fingerprintA, fingerprintB);
double fractionEqualBitsAC = // 0.4931640625
policy.getFractionOfEqualComponents(fingerprintA, fingerprintC);
double fractionEqualBitsBC = // 0.5048828125
policy.getFractionOfEqualComponents(fingerprintB, fingerprintC);
Speeding up Simhash by 10x using a bit hack was originally published in Dynatrace Engineering on Medium, where people are continuing the conversation by highlighting and responding to this story.
